algorithms

Bucket Sort

Arkar Min Tun

Apr 5, 2024 • 3 min read

Bucket sort ဆိုတာ နာမည်မှာ ပါတဲ့အတိုင်းပဲ input အနေနဲ့လာတဲ့ values တွေကို bucket လေးတွေခွဲထည့်ပြီး စီသွားတာမျိုးဖြစ်တယ်။ values တွေကို အစကနေ အဆုံးအထိ နှိုင်းယှဥ်ပြီး စီသွားတာမျိုးမဟုတ်ဘဲ bucket ထဲမှာ ခွဲထည့်ထားတာတွေကို စီပြီးမှ ပြန်ပေါင်းလိုက်တာမျိုး ဖြစ်တယ်။

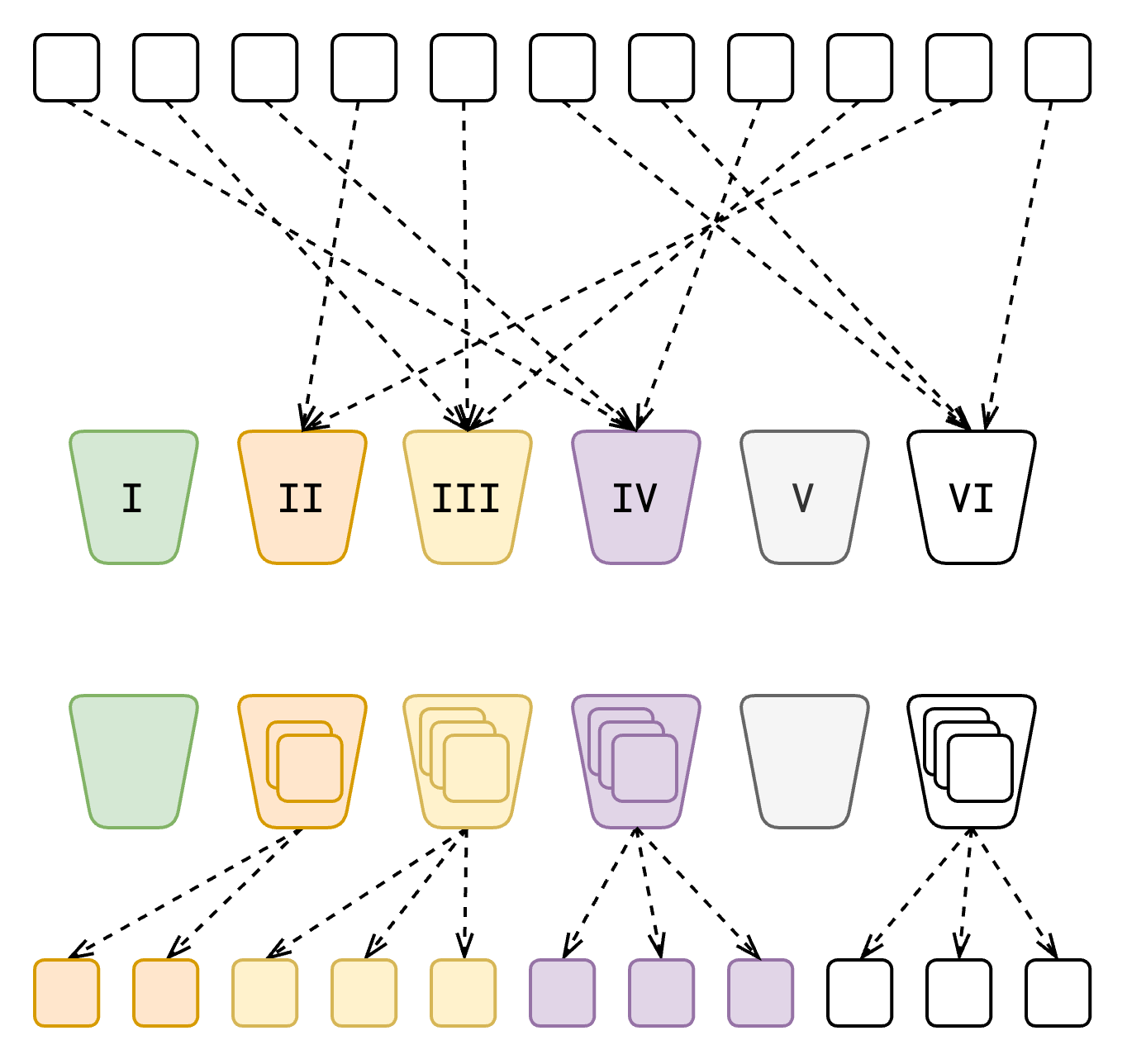
Bucket sort ကိုတော့ value တွေကို range တခု သတ်မှတ်လို့ရတဲ့နေရာမှာ သုံးသင့်ပါတယ်။ ဥပမာ အငယ်ဆုံးနဲ့ အကြီးဆုံး ဖြစ်နိုင်တဲ့ value တွေကို သိနိုင်တဲ့အချိန်မျိုးပေါ့။ ဘာလို့ သိဖို့လိုသလဲဆိုရင် bucket တွေအဖြစ် ဘယ်လို ခွဲမလဲဆိုတာ ဆုံးဖြတ်ဖို့ လိုတဲ့အတွက် ဖြစ်တယ်။ Bucket တခုထဲမှာ ရှိသမျှ input value တွေ အကုန် ရောက်သွားရင် bucket sort မဟုတ်တော့ဘူး ဖြစ်သွားလိမ့်မယ်။ integer လိုမျိုး value တွေကို စီဖို့လိုတဲ့အခါ bucket တွေကို 0 to 5, 5 to 10, 10 to 15 စသဖြင့် ခွဲသွားလို့ရမယ်။ 0 ကနေ စတာမျိုး မဟုတ်ဘဲ တခြား value ကနေ စတာလဲ ဖြစ်နိုင်တယ်။ ဒါကတော့ input value တွေပေါ်မူတည်မယ်။

တကယ်လို့ input value တွေက integer မဟုတ်ဘဲ floating point ဆိုရင်ရော ဘယ်လို ခွဲသွားလို့ ရမယ်ထင်လဲ? floating point တွေဆိုရင်တော့ ကျွန်တော်တို့ bucket 10 ခုခွဲပြီး သုံးသွားလို့ရမယ်။ floating point ဆိုတဲ့နေရာမှာ 0.34, 0.21, 0.56 အဲ့လိုမျိုးတွေကို ဆိုလိုတာဖြစ်တယ်။ ဒီလို အတိအကျ မဖြစ်နေလဲ point ကို နေရာရွှေ့ပြီး ခွဲလို့ရတဲ့အခါ အသုံးပြုလို့ရတယ်။ 0.34, 0.38, 0.31 အဲ့လို value တွေကို 3.4, 3.8, 3.1 စသဖြင့် ပြောင်းစစ်ပြီးတော့ နဂိုမူလ value ကို 3 ဆိုတဲ့ bucket ထဲမှာ စုထည့်တာမျိုးကို ပြောချင်တာပါ။

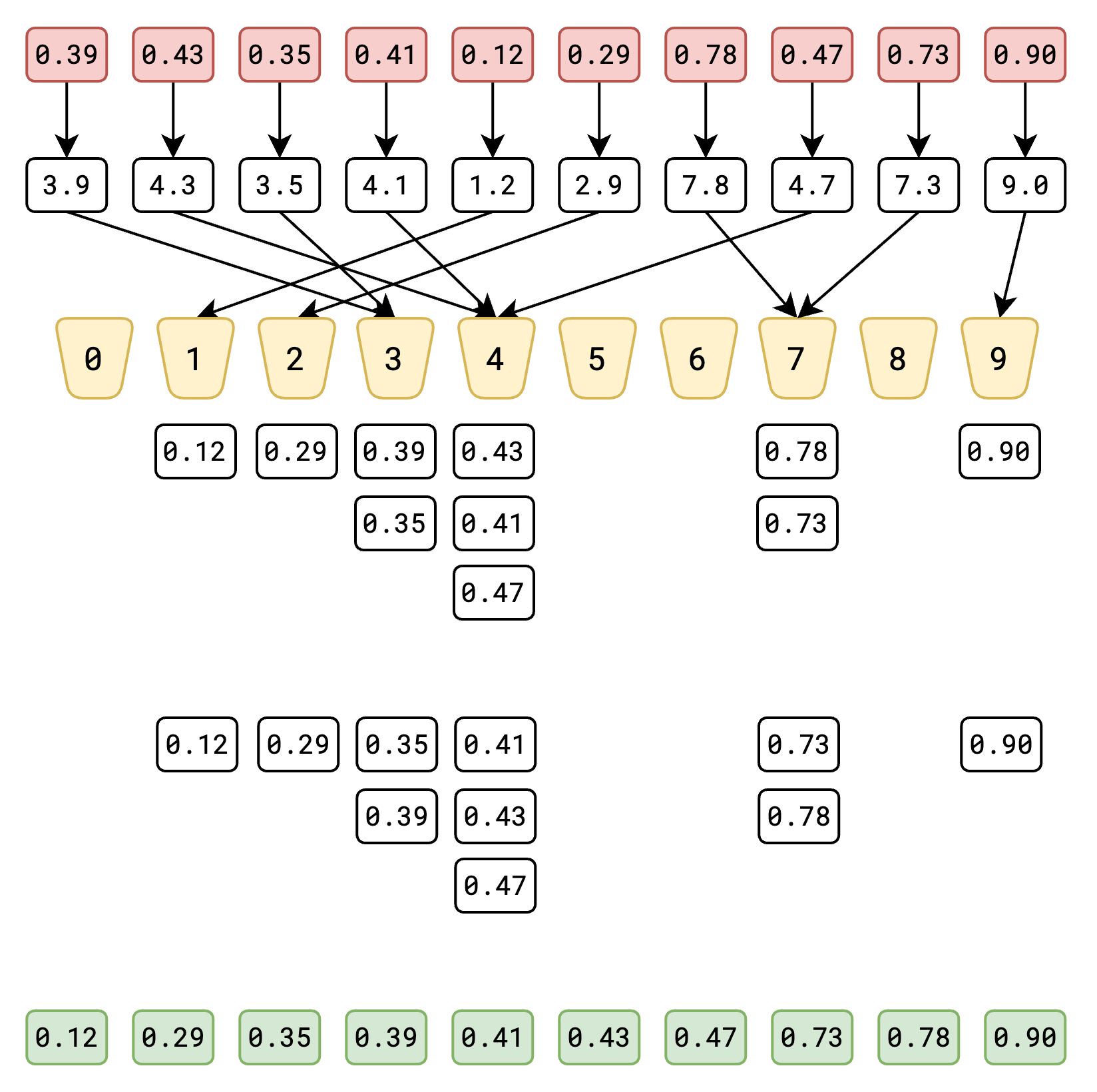
အပေါ်မှာ ပြထားသလိုပဲ bucket ထဲကို value တွေ ခွဲထည့်ပြီးတဲ့အခါ bucket တခုချင်းစီကို sorting လုပ်သွားမယ်။ ဒီမှာတော့ ကျွန်တော်တို့ အဆင်ပြေတဲ့ sorting algorithm ကို သုံးလို့ရတယ်။ Bucket Sort မှာ algorithm တခုထဲ မဟုတ်ဘဲ တခြား sorting algorithm တွေနဲ့ တွဲသုံးသွားရတဲ့ သဘောပါ။

Theory ပိုင်းကြည့်ပြီးပြီဆိုတော့ code နဲ့ ကြည့်ကြည့်ရအောင်ပါ။

const insertionSort = (bucket) => {
  let i, key, j;
  for (i = 1; i < bucket.length; i++) {
    key = bucket[i];
    j = i - 1;

    while (j >= 0 && bucket[j] > key) {
      bucket[j + 1] = bucket[j];
      j = j - 1;
    }
    bucket[j + 1] = key;
  }
};

const bucketSort = (arr) => {
  // Step 1: Create the buckets
  let buckets = Array.from({ length: 10 }, () => []);

  // Step 2: Determine the bucket and put the value in the bucket
  for (let i = 0; i < arr.length; i++) {
    let bucketIndex = Math.floor(10 * arr[i]);
    buckets[bucketIndex].push(arr[i]);
  }

  // Step 3: Sort each bucket in the bucket array
  for (let i = 0; i < buckets.length; i++) {
    insertionSort(buckets[i]);
  }

  // Step 4: Concatenate all buckets into arr[]
  let index = 0;
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < buckets[i].length; j++) {
      arr[index++] = buckets[i][j];
    }
  }

  return arr;
};

let arr = [0.39, 0.43, 0.35, 0.41, 0.12, 0.29, 0.78, 0.47, 0.73, 0.90];
console.log(bucketSort(arr));

[0.12, 0.29, 0.35, 0.39, 0.41, 0.43, 0.47, 0.73, 0.78, 0.90]

အပေါ်မှာ ရှင်းပြသွားသလိုပဲ အဆင့်၄ဆင့် ပါဝင်ပါတယ်။ ပထမဆုံးအဆင့်ကတော့ buckets array တည်ဆောက်တာပဲ ဖြစ်ပါတယ်။ ဒီမှာ floating point နဲ့ value တွေ ဝင်လာတာ ဖြစ်တဲ့အတွက် array length 10 နဲ့ တန်းပြီးတော့ buckets ဆိုတဲ့ array ကို ဆောက်လိုက်တာပဲ ဖြစ်ပါတယ်။

ဒုတိယအဆင့်မှာတော့ ဝင်လာတဲ့ value တွေကို သက်ဆိုင်ရာ bucket ထဲကို ထည့်ဖို့ပဲ ဖြစ်ပါတယ်။ ဒီမှာတော့ floating point ဖြစ်တဲ့အတွက် ၁၀ နဲ့မြှောက်ပြီးတော့ သူတို့ကို ထည့်ရမယ့် bucket index ကို ရှာထားတာပဲ ဖြစ်ပါတယ်။

value =  0.39
value * 10 = 3.9
Math.floor(value * 10) = 3 <- bucket index

တတိယအဆင့်မှာတော့ ကျွန်တော်တို့ အဆင်ပြေတဲ့ sorting algorithm နဲ့ bucket တခုချင်းစီကို sort လုပ်ပါမယ်။ အခုတော့ insertion sort ကို အသုံးပြုပြီး sort လုပ်သွားပါမယ်။ တခြား algorithm တွေကိုလဲ အသုံးပြုလို့ ရပါတယ်။ insertion sort အကြောင်းကို အောက်မှာ ပေးထားတဲ့ link မှာ သွားဖတ်လို့ရပါတယ်။

ဒါတွေအကုန်ပြီးပြီဆိုရင်တော့ sort လုပ်ထားတဲ့ bucket တွေထဲက value တွေကို ပြန်ပေါင်းဖို့ပဲ ကျန်ပါတော့တယ်။ bucket တခုချင်းစီထဲမှာ sort လုပ်ပြီးသားဖြစ်တာကြောင့် bucket အစီအစဥ်အလိုက်ပဲ value တွေကို ပေါင်းလိုက်တဲ့အခါ sort လုပ်ပြီးသား array ကို ရရှိပြီပဲ ဖြစ်ပါတယ်။

ဘယ်လိုအလုပ်လုပ်သလဲ နားလည်ပြီဆို bucket sort ရဲ့ complexity တွေ ဘယ်လို ရှိသလဲ ကြည့်ကြည့်ရအောင်ပါ။

Best Case Time Complexity: O(n+k)
Average Case Time Complexity: O(n)
Worst Case Time Complexity: O(n²)

Best Case Time Complexity

တကယ်လို့ ပေးလိုက်တဲ့ input value တွေကို bucket တွေထဲ ခွဲထည့်လိုက်လို့ bucket တခုချင်းစီမှာ ရောက်သွားတာက အကုန် အညီအမျှ (uniformly distributed) ဖြစ်နေတယ်ဆိုရင်တော့ best case time complexity ကို ရရှိနိုင်မှာပဲ ဖြစ်ပါတယ်။ input value တွေကို traverse လုပ်ပြီး bucket တွေထဲ ထည့်ဖို့က O(n) complexity လိုအပ်ပါတယ်။

အပေါ်မှာ ပြထားသလိုမျိုး bucket တခုချင်းစီကို insertion sort လိုမျိုး အသုံးပြုပြီး sort မယ်ဆိုရင်တော့ O(k) ဖြစ်သွားမှာပဲ ဖြစ်ပါတယ်။ ဒီနေရာမှာ n လို့ မသုံးဘဲ k ဆိုပြီး သုံးတာက n က input မှာ ပါလာတဲ့ value အရေအတွက်ဖြစ်ပြီး k က bucket တွေရဲ့ အရေအတွက်ကို ပြောချင်တာကြောင့် ခွဲပြီး ပြောတာပဲဖြစ်တယ်။ best case ဖြစ်တဲ့အချိန်မှာ value တွေကို tranverse လုပ်ပြီး sort လုပ်တာကလဲ bucket တခုနဲ့တခု အတူတူ constant time နီးပါး ရှိပါတယ်။ ဒီတော့ best case ဖြစ်တဲ့အခါ O(n) နဲ့ O(k) စုစုပေါင်းကို O(n+k) ဆိုပြီး ရရှိမှာပဲ ဖြစ်ပါတယ်။ တကယ့်လက်တွေ့မှာတော့ best case က ဖြစ်ခဲပါတယ်။

Average Case Time Complexity

ပေးလိုက်တဲ့ input value တွေကို bucket တွေထဲ ခွဲထည့်လိုက်လို့ bucket တခုချင်းစီမှာ ရောက်သွားတာက မညီမမျှ (randomly distributed) ဖြစ်နေတယ်ဆိုရင်တော့ average time complexity ကို ရရှိမှာ ဖြစ်ပါတယ်။ တချို့ bucket တွေမှာ value တွေက ရှိနေပြီး တချို့မှာ ရှိမနေတာမျိုး ဖြစ်နိုင်ပါတယ်။ ဒါကို average ပြန်ချလိုက်ရင် constant time အဖြစ် သတ်မှတ်နိုင်တဲ့အတွက် complexity ကို O(n) ဆိုပြီး ရရှိမှာ ဖြစ်ပါတယ်။

Worst Case Time Complexity

Bucket တွေထဲ ခွဲထည့်တဲ့အခါ အခြေအနေတခုခုကြောင့် bucket တချို့မှာ value တွေအများကြီး ရောက်သွားတဲ့အခါ worst case ဖြစ်နိုင်ပါတယ်။ ဒီလိုအခြေအနေမှာတော့ bucket ကို sort တာကလဲ ပေးလိုက်တဲ့ input value တွေနီးပါများပြီးတော့ ကြာသွားနိုင်ပါတယ်။ ကိုယ်လိုချင်တဲ့ order ရဲ့ ဆန့်ကျင်ဘက်အနေနဲ့ဆို value တွေ အကုန်နီးပါးကို နေရာရွှေ့ပြီး စီသွားရတော့မှာပဲ ဖြစ်ပါတယ်။ ဒီအခြေအနေမှာဆိုရင် တော့ O(n²) ဆိုပြီး ရရှိမှာပဲ ဖြစ်ပါတယ်။

Space Complexity

ကျွန်တော်တို့တွေ ပေးလိုက်တဲ့ input value တွေကို bucket တွေထဲ ခွဲထည့်တဲ့အတွက် bucket တွေအတွက် နေရာလိုသလို value တွေအတွက်လဲ နေရာလိုပါတယ်။ ဒီတော့ O(n+k) space complexity ကို ရရှိမှာဖြစ်ပြီး n ကတော့ input value အရေအတွက်နဲ့ k ကတော့ bucket အရေအတွက်ပဲ ဖြစ်ပါတယ်။