Counting Sort

Counting sort ဆိုတာကတော့ နာမည်မှာပါတဲ့အတိုင်းပဲ value တွေကို ရေတွက်တာကို အခြေခံပြီး တည်ဆောက်ထားတဲ့ sorting algorithm တခုပဲ ဖြစ်ပါတယ်။ သူ့ကိုတော့ decimal တွေကို sort တဲ့နေရာတွေ၊ value တူတာ ထပ်တာတွေ မပါတဲ့အချိန်တွေမှာ သုံးလို့ အဆင်မပြေပါဘူး။ value တူတာတွေ ပါတာများပြီးတော့ စီရတဲ့အချိန်ဆိုရင်တော့ သုံးလို့ရပါတယ်။ ဘာလို့လဲဆိုတော့ value ထပ်တာတွေကို ရေတွက်ပြီး တွက်ချက်ထားတဲ့အတွက် ဖြစ်ပါတယ်။ ဘယ်လို အလုပ်လုပ်သလဲ ကြည့်ကြည့်ရအောင်ပါ။

ပထမဆုံး ကျွန်တော်တို့ ပေးလိုက်တဲ့ input value ထဲမှာ အကြီးဆုံး value ကို ရှာပါမယ်။

ဒီ ဥပမာမှာတော့ နံပါတ် ၇ က အကြီးဆုံးအနေနဲ့ ရှိနေပါတယ်။ အကြီးဆုံး value ကို ရပြီဆို အကြီးဆုံး value ကို ၁ပေါင်းပြီး array အသစ်တခု တည်ဆောက်လိုက်ပါမယ်။ အခု လက်ရှိမှာ အကြီးဆုံး value က ၇ ဖြစ်တဲ့အတွက် အခန်း ၈ ခန်းပါတဲ့ array တခုကို တည်ဆောက်လိုက်ပါမယ်။ တကယ်လို့ အကြီးဆုံး value က အခြား value တွေဖြစ်နေတယ်ဆိုလဲ အဲ့ဒီ value ကို ၁ ပေါင်းပြီး array အသစ်တခု တည်ဆောက်ရပါမယ်။ array ထဲမှာ default value အနေနဲ့ 0 တွေကို ထည့်ထားပါမယ်။

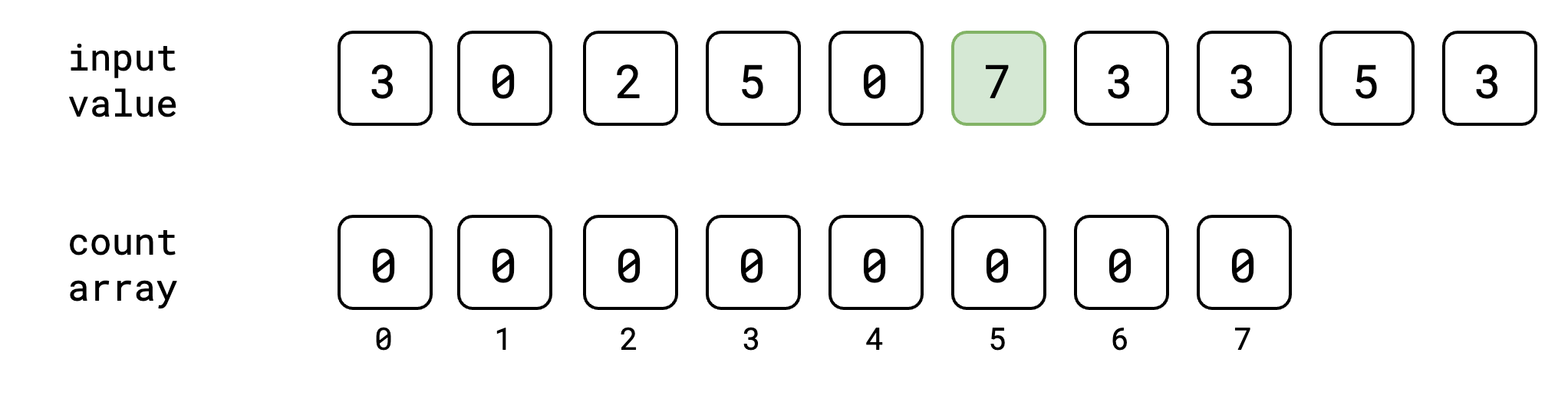
ပြီးရင်တော့ count array ထဲမှာ input value တွေကို index အနေနဲ့ ယူပြီး သိမ်းပါမယ်။ အစဆုံး value 3 အတွက်ဆို count array ရဲ့ index 3 မှာ ၁ တိုးပြီး သိမ်းပါမယ်။

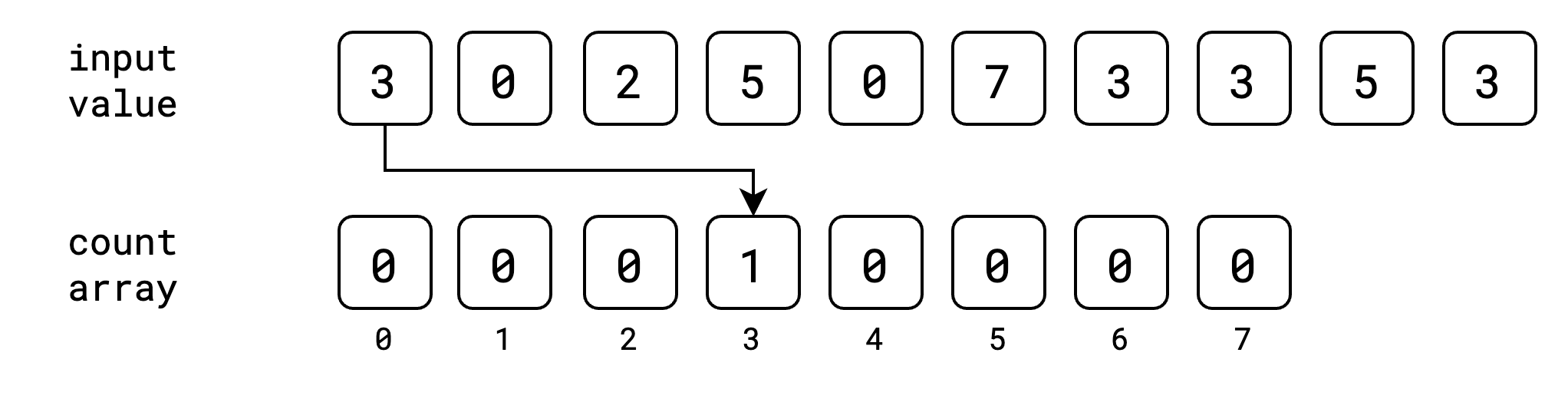
ဒုတိယ value 0 အတွက် index 0 မှာ ၁တိုးပါမယ်။

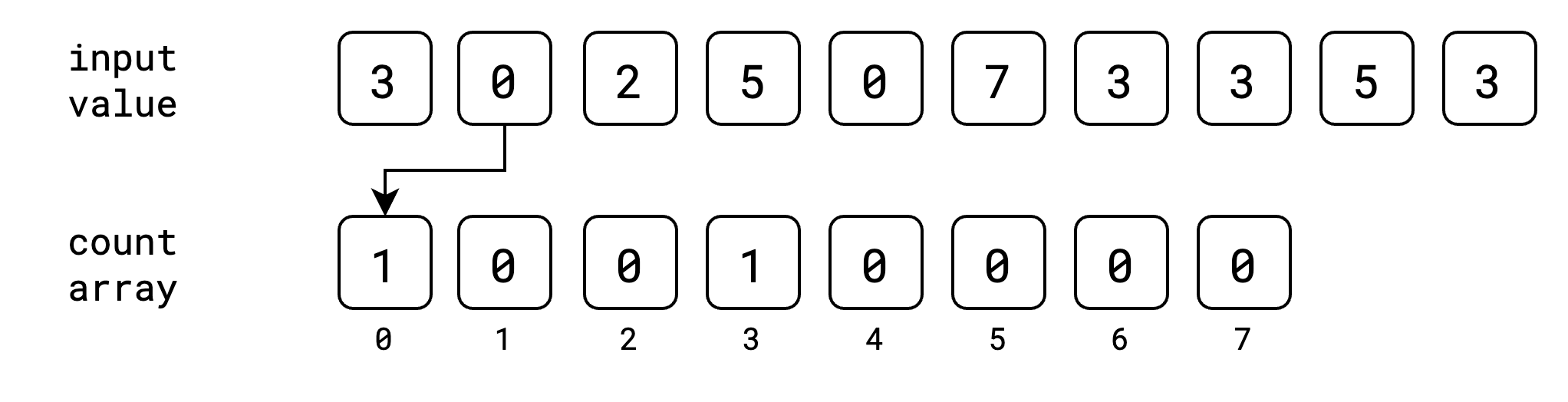
ဒီလိုနဲ့ input value အကုန်အတွက် index အလိုက် value တွေကို count array ထဲမှာ တိုးပြီး သိမ်းသွားပါမယ်။

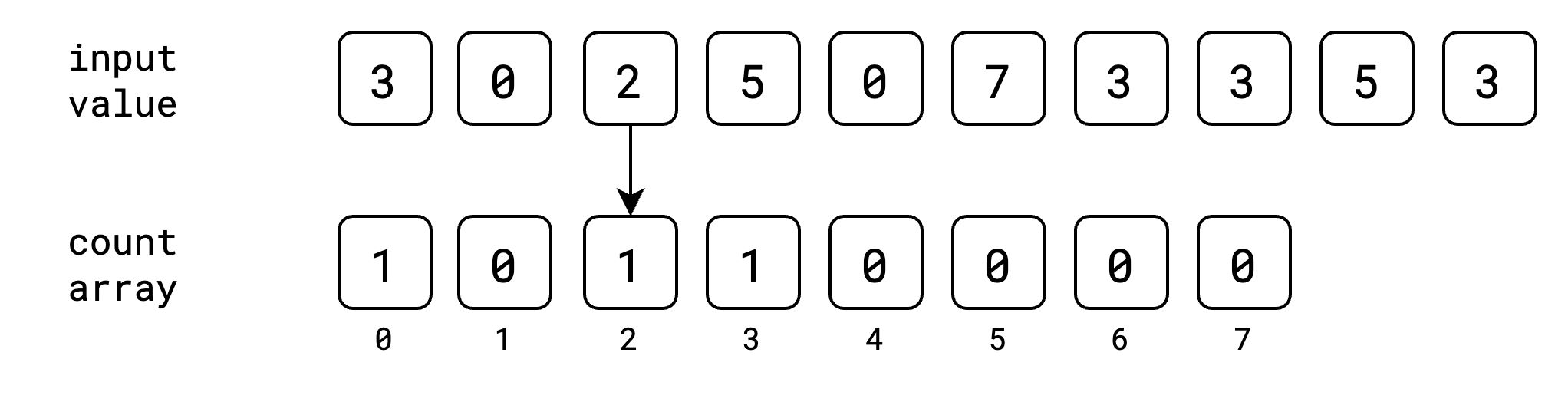
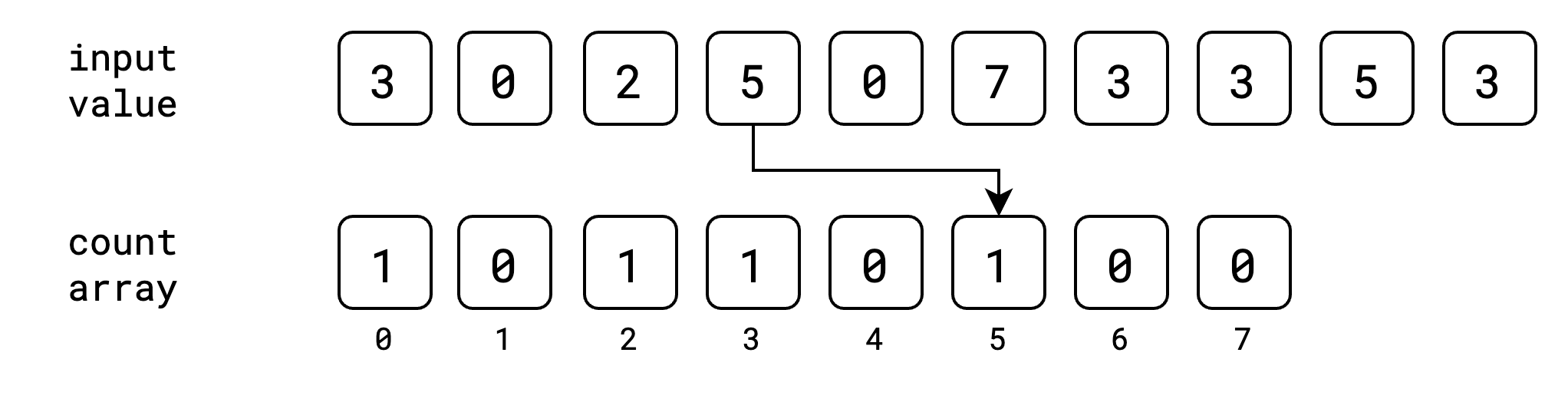
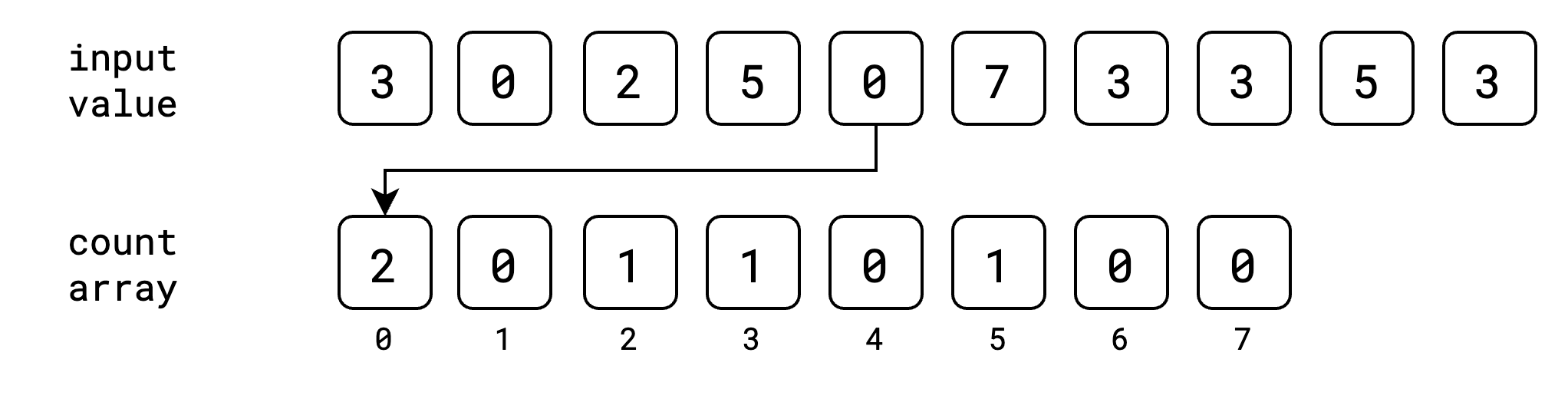
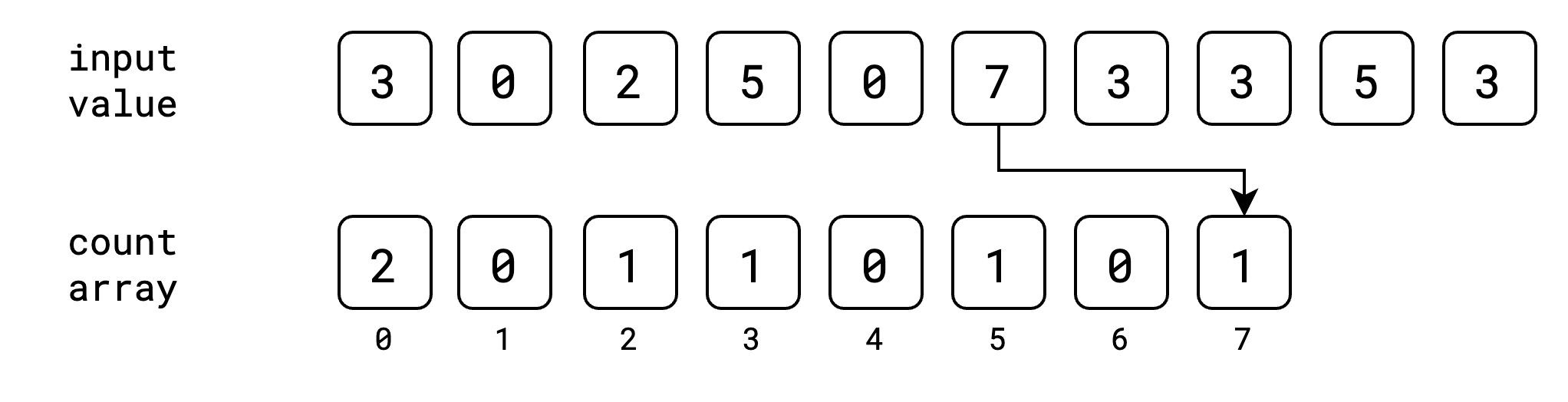
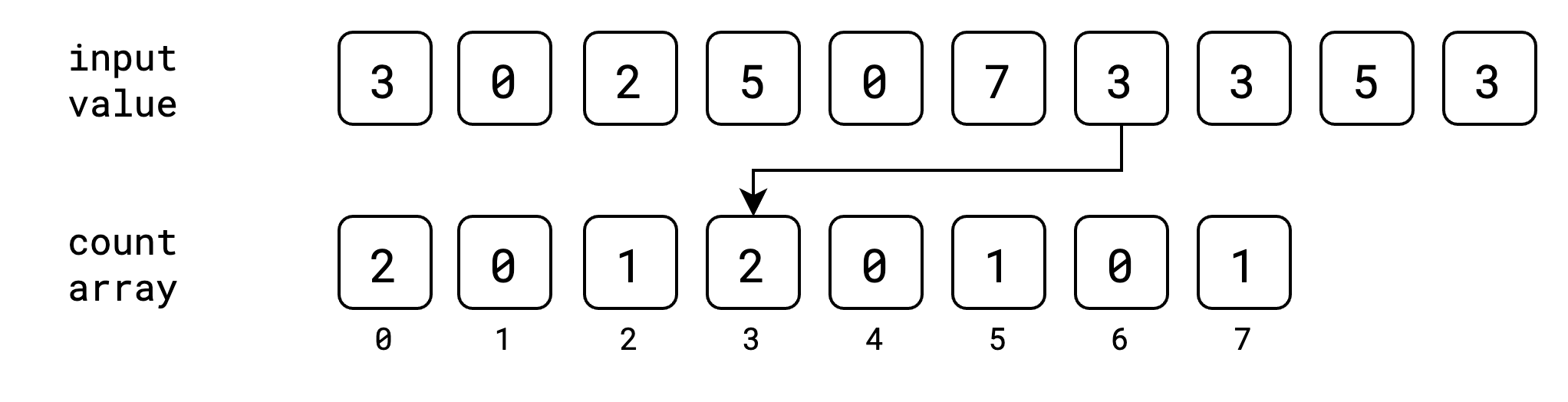
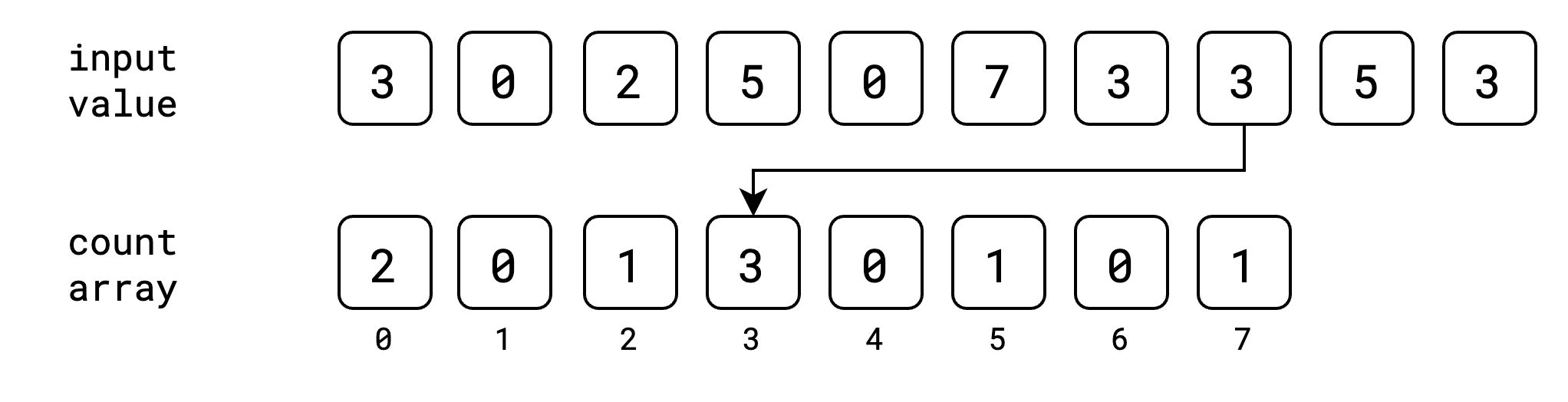
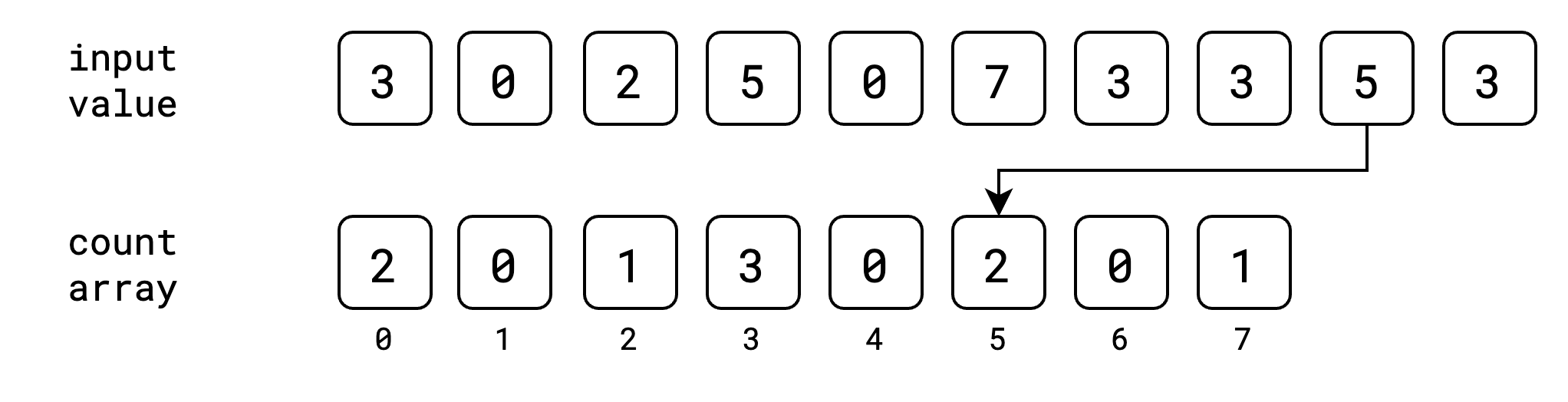
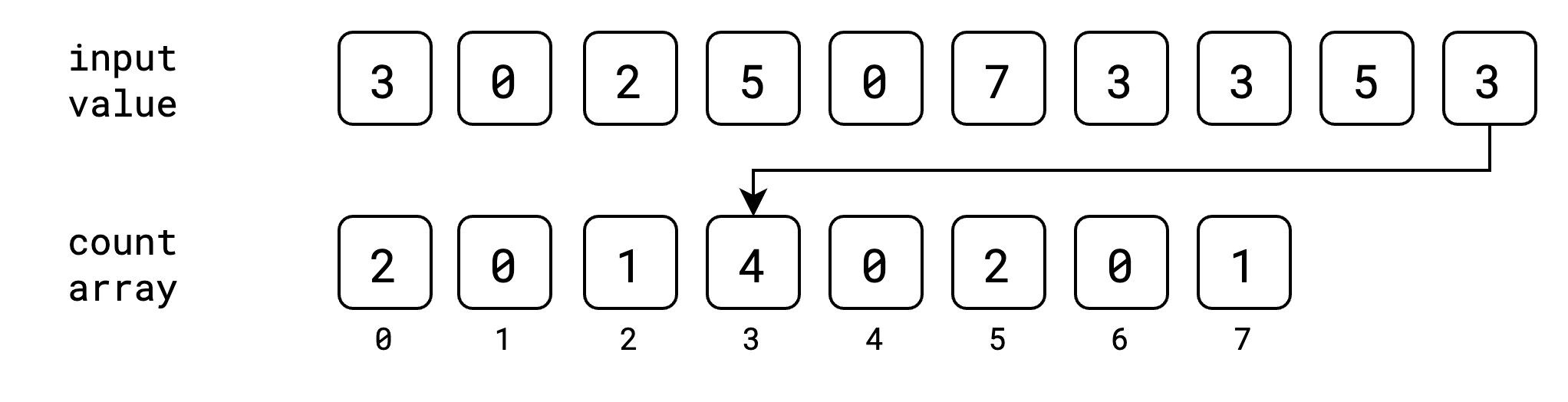
အခုအဆင့်မှာတော့ input value တွေ အကုန်လုံးကို သူတို့နဲ့ သက်ဆိုင်တဲ့ index တွေမှာ ဘယ်နှစ်ခေါက်ထပ်ပြီး ပါလာသလဲဆိုတာ မှတ်ထားပြီးပါပြီ။ ဒါပြီးရင်တော့ count array မှာ cumulative sum/prefix sum ကို တွက်ထုတ်ရပါမယ်။ cumulative sum ဆိုတာကတော့ ရှေ့ဆုံးကနေ လက်ရှိနေရာအထိ value တွေရဲ့ ပေါင်းလဒ်ကို ပြောတာပဲ ဖြစ်ပါတယ်။ ဥပမာ index 3 နေရာရဲ့ cumulative sum ဆိုရင် index 0, 1, 2, 3 တို့ရဲ့ပေါင်းလဒ်ပဲ ဖြစ်ပါတယ်။ count array ရဲ့ cumulative sum ကို အခုလိုမျိုး ရရှိမှာ ဖြစ်ပါတယ်။

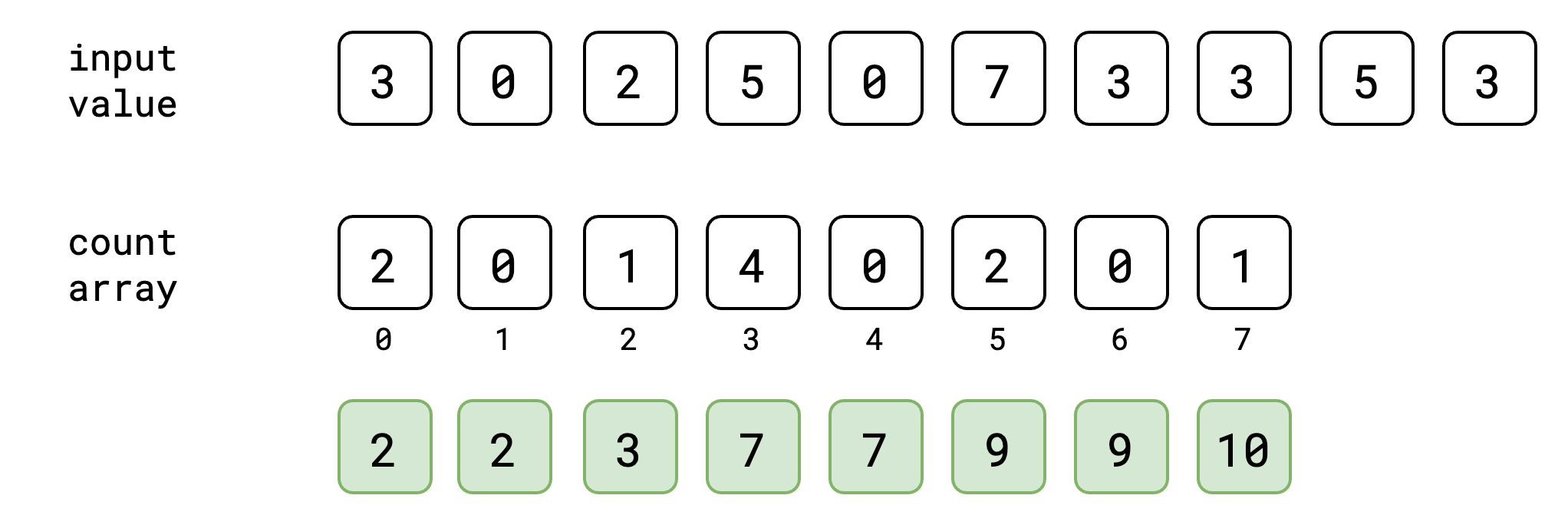
အခုလို တွက်ပြီးပြီဆိုရင်တော့ output value ကို တွက်ထုတ်ဖို့ အဆင်သင့်ဖြစ်ပါပြီ။ output value ကလဲ input value နဲ့ size အတူတူ ထွက်လာမှာ ဖြစ်တဲ့အတွက် size တူတဲ့ array တခု တည်ဆောက်လိုက်ပါမယ်။

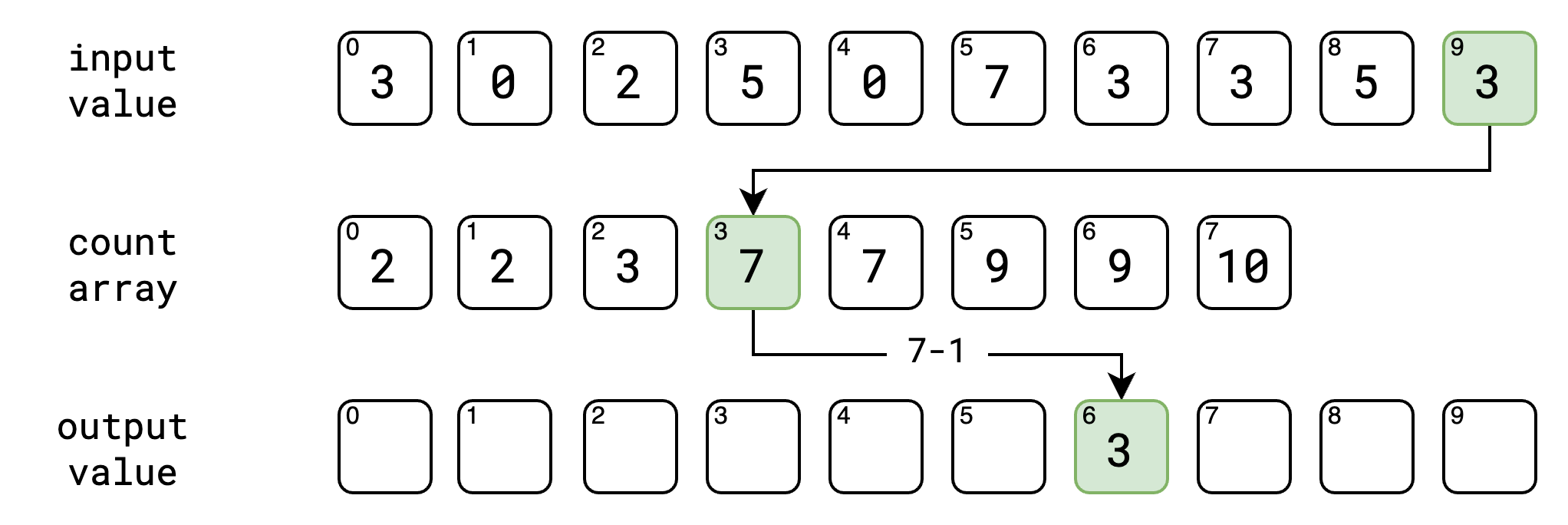
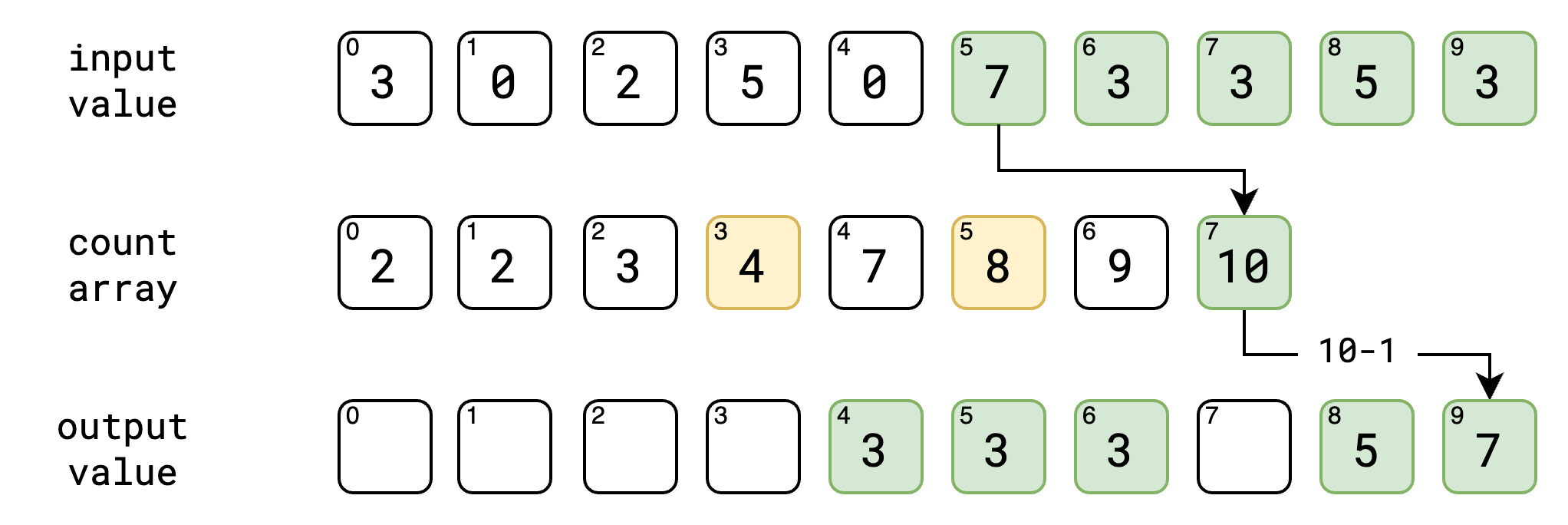
ဒီ step မှာတော့ အနည်းငယ် ရှုပ်သယောင် ရှိပါတယ်။ input value ကိုပဲ ကျွန်တော်တို့တွေ နောက်ဆုံးကနေ ရှေ့ဆုံးအထိ traverse လုပ်သွားပါမယ်။ ဥပမာ input value ရဲ့ နောက်ဆုံး နံပါတ် ၃ ဆိုပါစို့။ input value ရဲ့ လက်ရှိ value က count array ရဲ့ index အနေနဲ့ ဖြစ်သွားပါမယ်။ count array ရဲ့ index ကို ရပြီဆို ကျွန်တော်တို့ အဲ့ဒီ့ index မှာ ရှိတဲ့ value ကို ၁ နှုတ်လိုက်ပါမယ်။ အပေါ်မှာ နောက်ဆုံး နံပါတ် ၃ ကို count array မှာ ကြည့်မယ်ဆို နံပါတ် ၇ ကို ရရှိမှာပဲ ဖြစ်ပါတယ်။ count array ရဲ့ index နံပါတ် ၃ မှာ ရှိနေတဲ့ value က ၇ ဖြစ်နေလို့ပဲ ဖြစ်ပါတယ်။ အဲ့ဒီမှာ ရလာတဲ့ value ကို ၁နှုတ်လိုက်တဲ့အခါ output value ရဲ့ index ကို ရရှိပါမယ်။ အပေါ်မှာ ရတဲ့ နံပါတ် ၇ ကို ၁နှုတ်လိုက်ရင် ၆ ကို ရမှာ ဖြစ်ပါတယ်။ အဲ့ index နံပါတ်မှာ ကျွန်တော်တို့ input value က ရလာတဲ့ value ကို သွားထည့်မှာပဲ ဖြစ်ပါတယ်။ အခု output value ရဲ့ index နံပါတ် ၆ မှာ input value က ရလာတဲ့ နံပါတ် ၃ ကို ထည့်လိုက်ပါမယ်။ count array မှာလဲ ၁လျှော့လိုက်တဲ့ နံပါတ်ကို မှတ်လိုက်ပါမယ်။

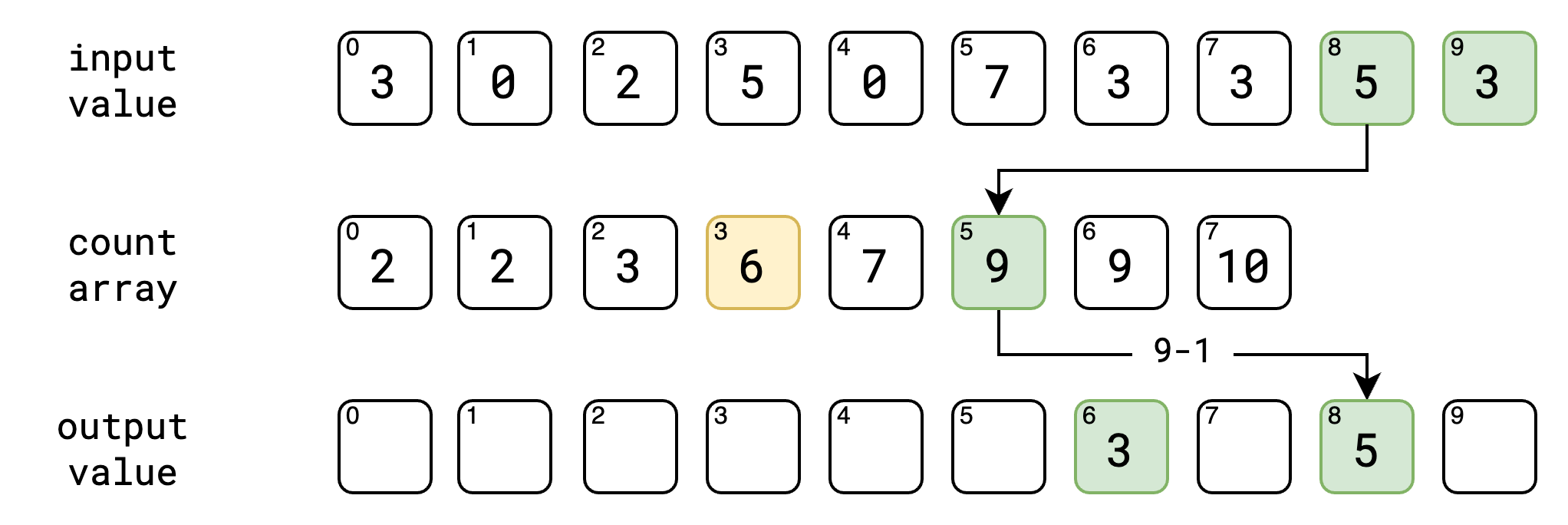
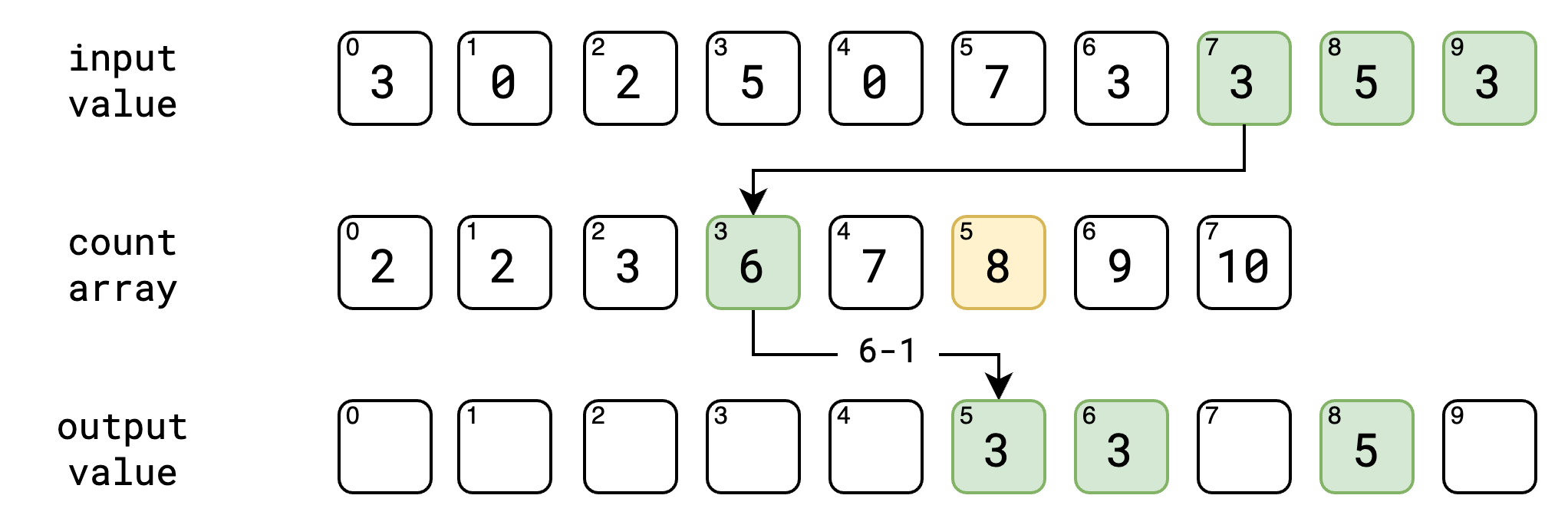
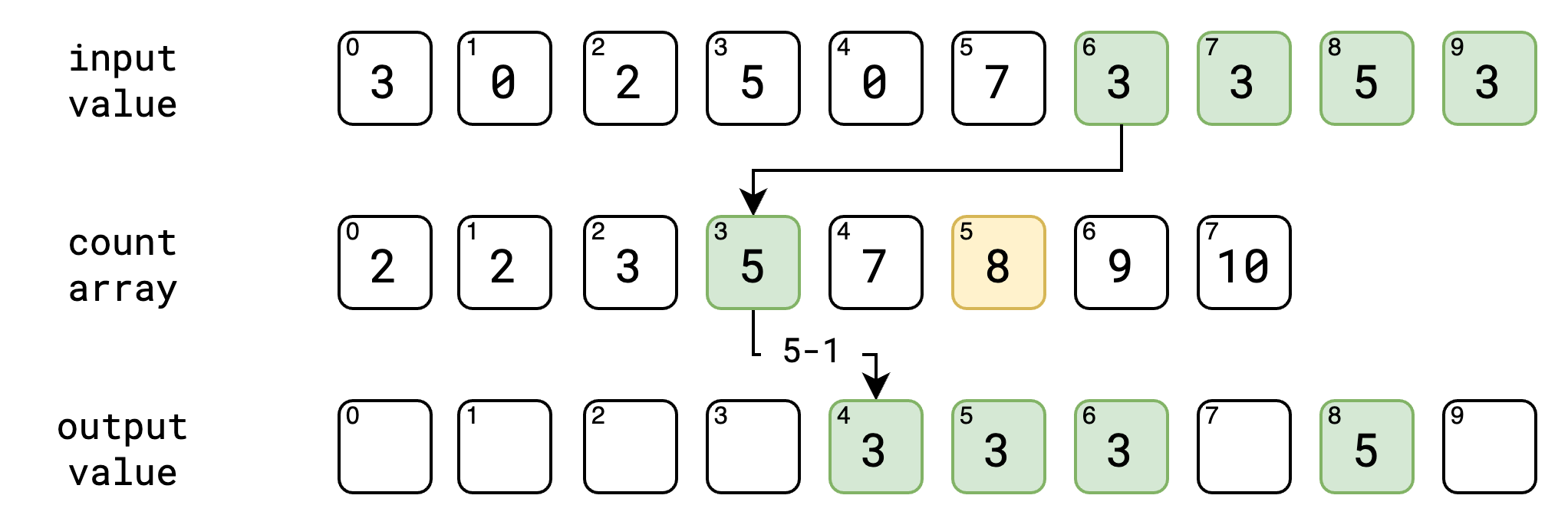
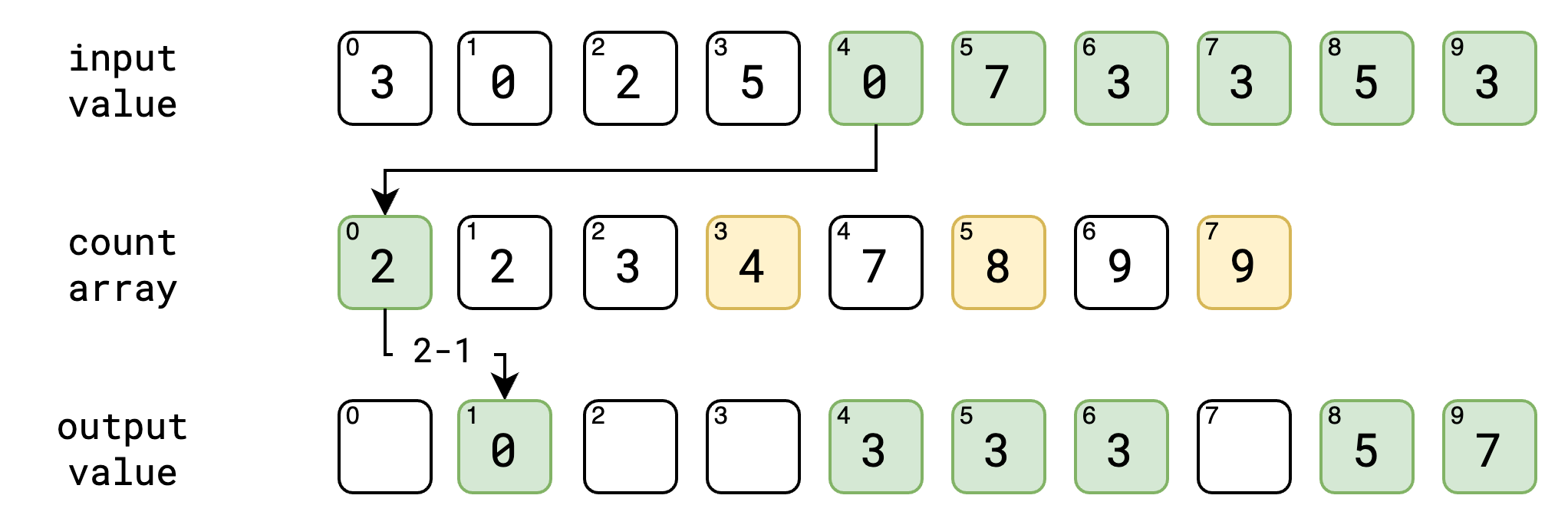
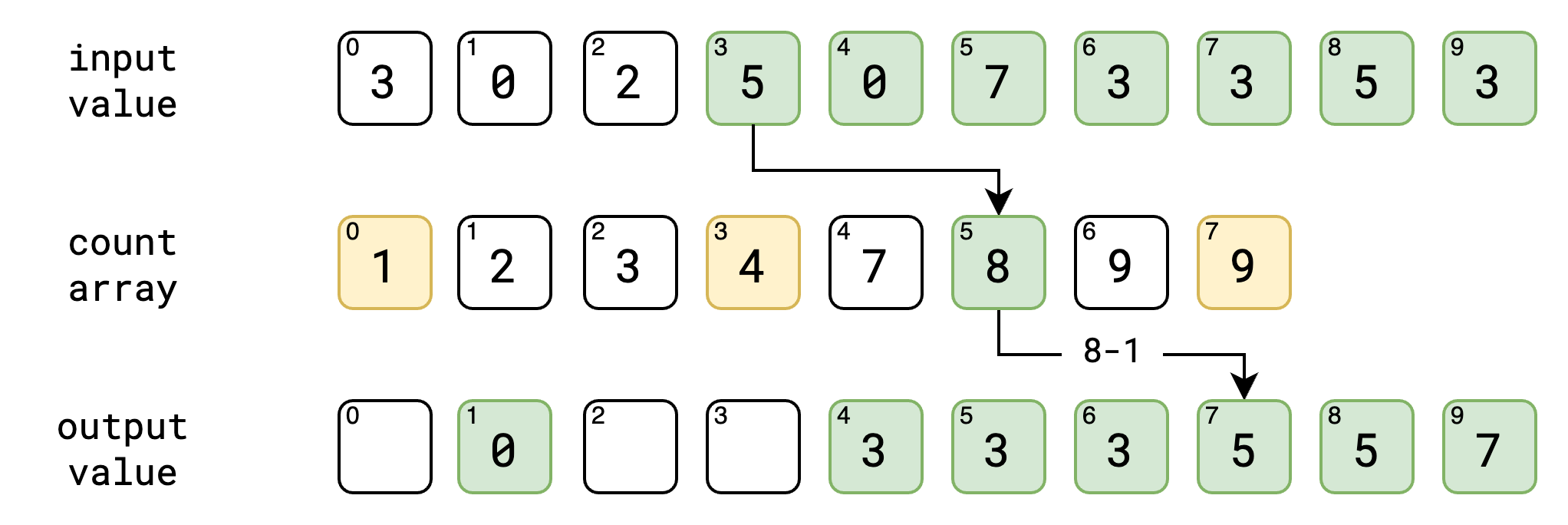
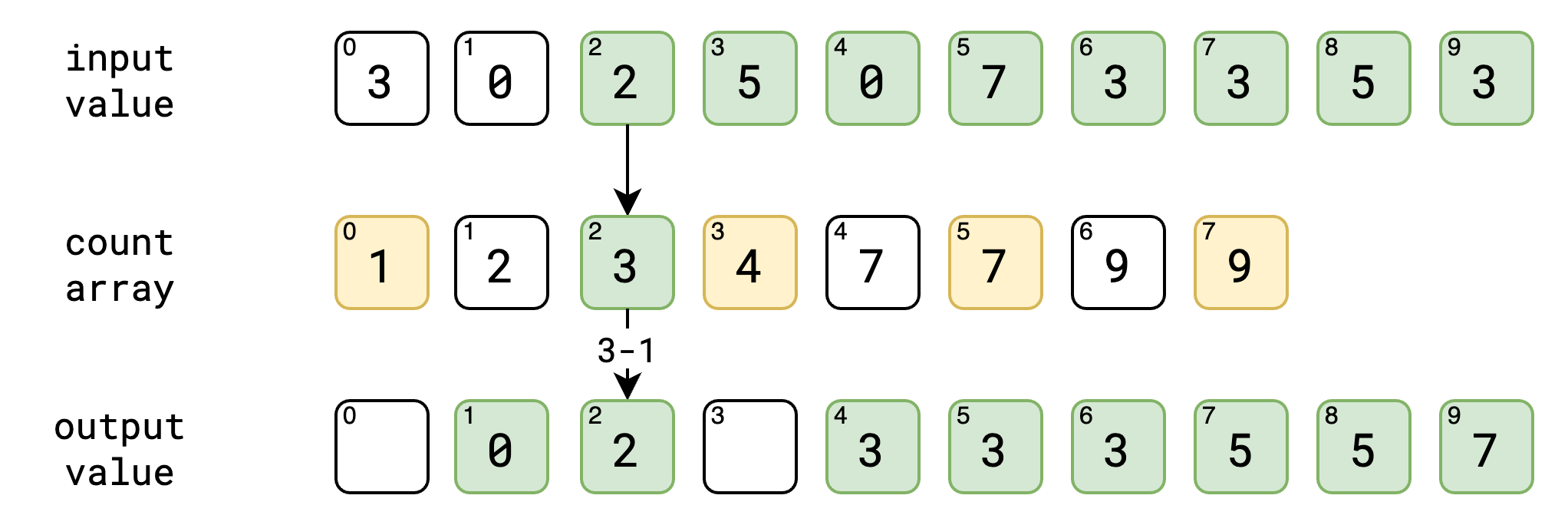
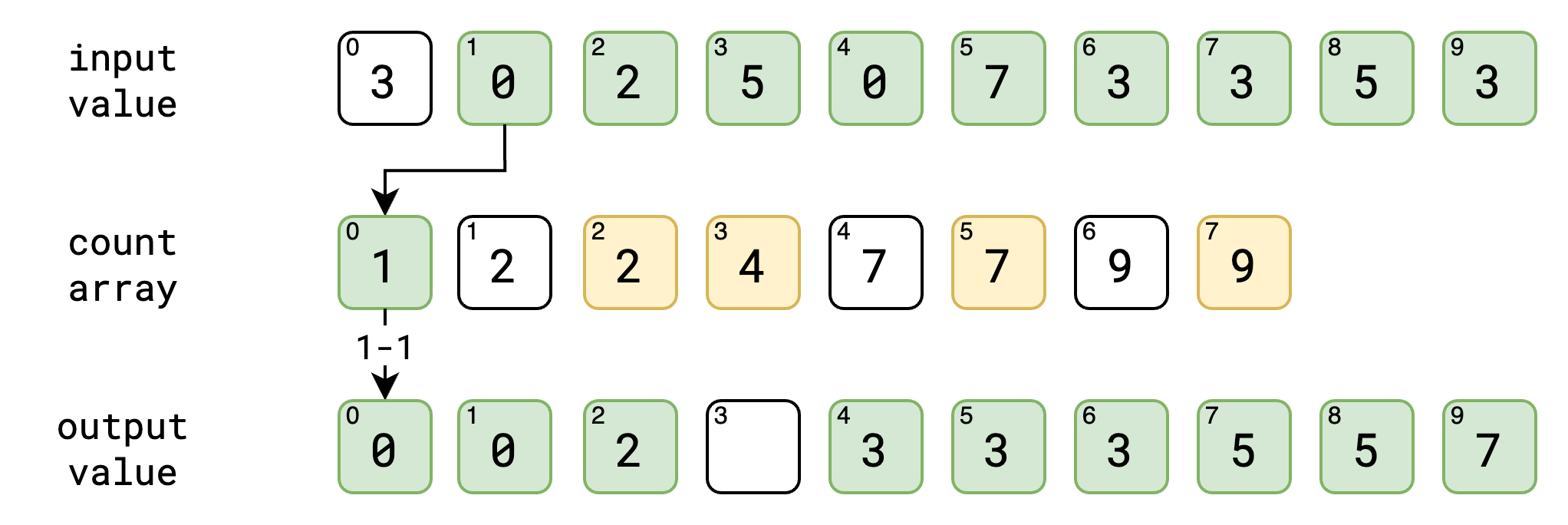
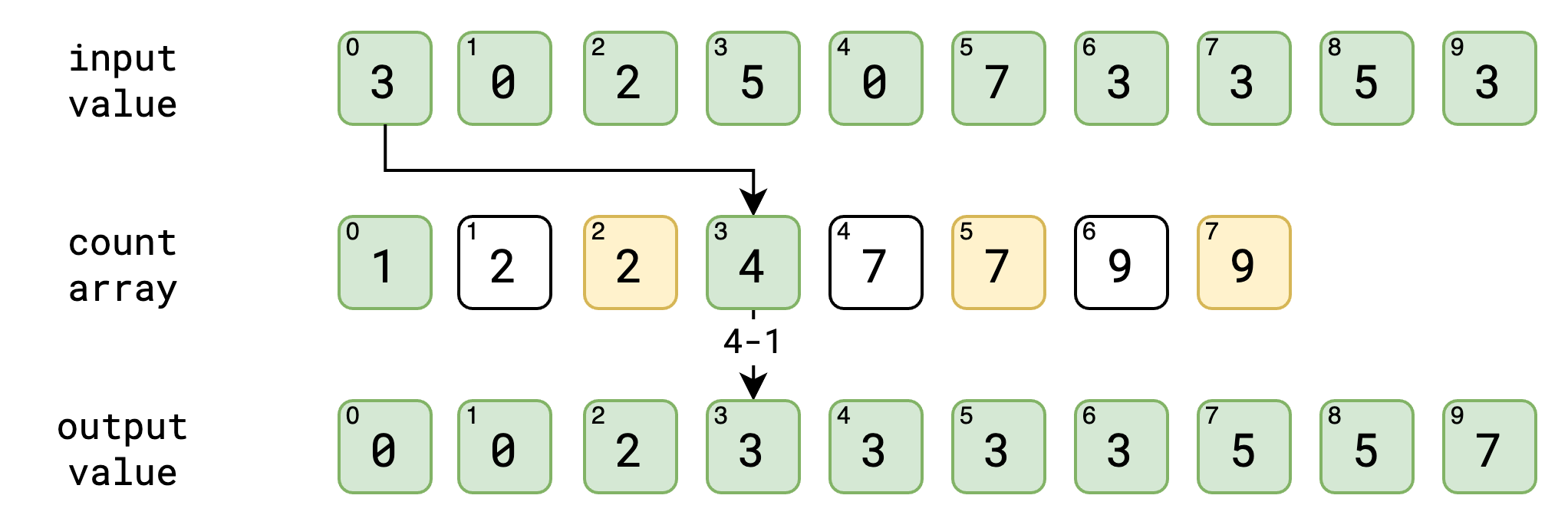
ဒါတွေအကုန် ပြီးသွားရင်တော့ ကျွန်တော်တို့ လိုချင်တဲ့ output value ကို sort လုပ်ပြီးတဲ့ အနေအထားနဲ့ ရရှိပြီပဲ ဖြစ်ပါတယ်။

Code အနေနဲ့ ဘယ်လိုရေးမလဲ​ ကြည့်ကြည့်ရအောင်ပါ။

const countingSort = (inputValue) => {
  const inputLength = inputValue.length;
  const maxValue = Math.max(...inputValue);
  const countArray = new Array(maxValue + 1).fill(0);

  for (let i = 0; i < inputLength; i++) {
      countArray[inputValue[i]]++;
  }

  for (let i = 1; i <= maxValue; i++) {
      countArray[i] += countArray[i - 1];
  }

  const outputValue = new Array(inputLength);
  for (let i = inputLength - 1; i >= 0; i--) {
    outputValue[countArray[inputValue[i]] - 1] = inputValue[i];
      countArray[inputValue[i]]--;
  }

  return outputValue;
}

const inputValue = [3, 0, 2, 5, 0, 7, 3, 3, 5, 3];
console.log(countingSort(inputValue));

[0, 0, 2, 3, 3, 3, 3, 5, 5, 7]

Time Complexity

Time complexity ကို ကြည့်မယ်ဆို input value ရဲ့ size ဘယ်လိုပဲဖြစ်စေ ကျွန်တော်တို့ input value နဲ့ count array တွေကို traverse လုပ်မှာ ဖြစ်တဲ့အတွက် O(n+k) ကို ရရှိမှာ ဖြစ်ပါတယ်။ n ကတော့ input value ရဲ့ length ဖြစ်ပြီး k ကတော့ count array ရဲ့ length ပဲ ဖြစ်ပါတယ်။

• Worst Case: O(n+k)
• Average Case: O(n+k)
• Best Case: O(n+k)

Space Complexity

Space complexity ကို ကြည့်မယ်ဆိုလဲ ကျွန်တော်တို့မှာ input value နဲ့ size တူတဲ့ output value အတွက်နဲ့ count array တို့အတွက် space တွေ လိုအပ်မှာ ဖြစ်ပါတယ်။ ဒီတော့ space complexity အနေနဲ့ O(n+k) ကို ရရှိမှာ ဖြစ်ပါတယ်။