Merge Sort

Merge sort ဆိုတာ sorting algorithm တွေထဲက တခုဖြစ်ပြီးတော့ divide & conquer လို့အပြောများတဲ့ recursive (ဆင့်ကာ ဆင့်ကာ) ခေါ်တဲ့နည်းကို အသုံးပြုထားတဲ့ algorithm ပဲ ဖြစ်ပါတယ်။ ပေးထားတဲ့ array ကို အဆင့်ဆင့် ခွဲချပြီးတော့ အသေးဆုံးအပိုင်းကနေ စီသွားတာမျိုးပဲ ဖြစ်ပါတယ်။ ဥပမာ ပေးထားတဲ့ array ထဲမှာ value လေးခုပါတယ်ဆို အရင်ဆုံး ၂ခုစီ ခွဲချလိုက်တယ်။ အဲ့ဒီ ၂ခုဆီ ခွဲချထားတာကိုမှ တခုဆီ ဖြစ်အောင်အထိ ခွဲချပြီး အစီအစဥ်အလိုက် ပြန်ပေါင်းလိုက်တာမျိုးပဲ ဖြစ်ပါတယ်။

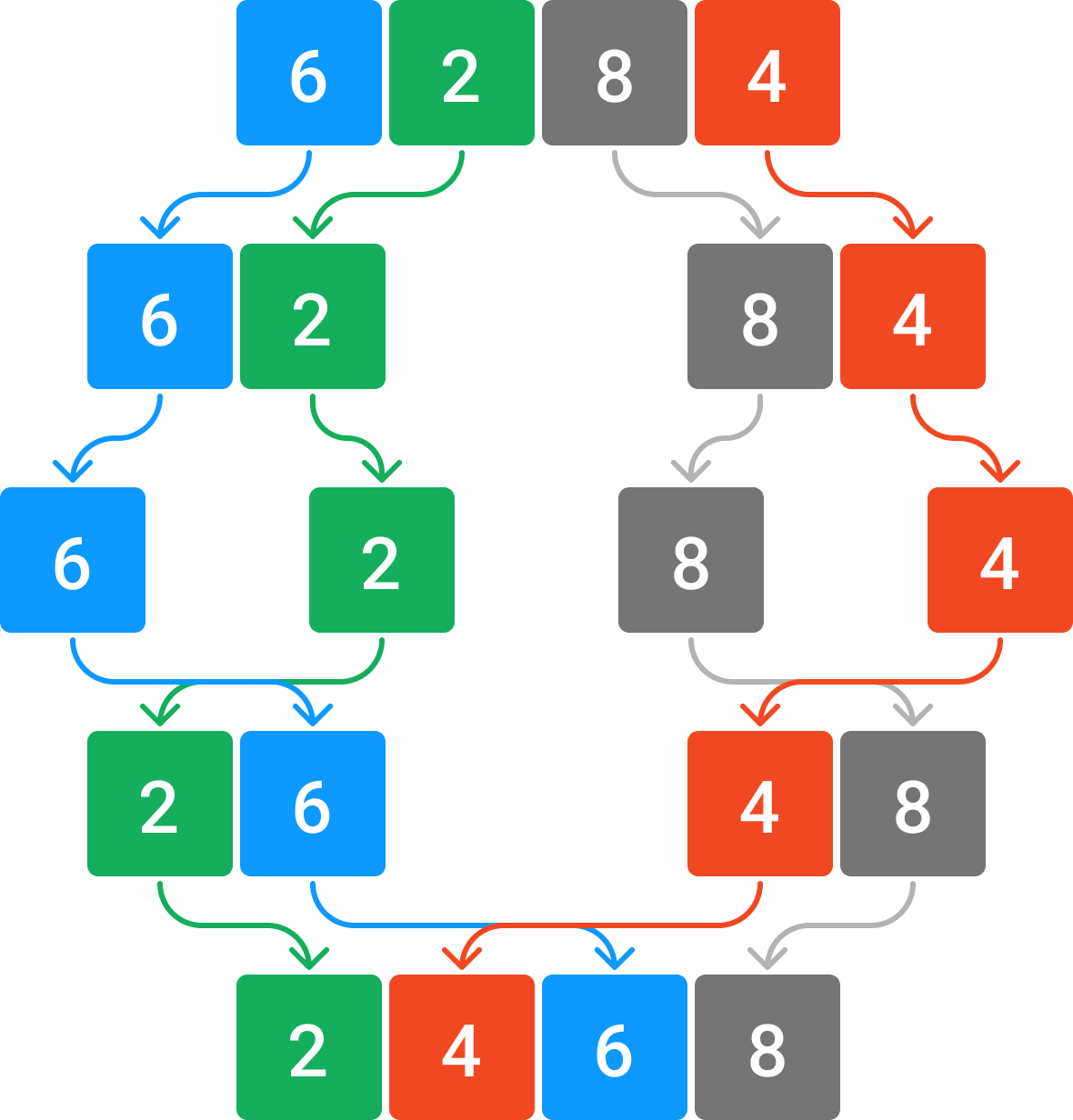
Merge sort ရဲ့ အလုပ်လုပ်ပုံ ကိုနားလည်ပြီဆို ပိုပြီး ရှုပ်ထွေးတဲ့ array example နောက်တခုလောက်နဲ့ ထပ်ပြီး ကြည့်ကြည့်ရအောင်ပါ။

အရင်ဆုံး ပေးထားတဲ့ array ကို ၂ပိုင်း ခွဲလိုက်မှာ ဖြစ်ပါတယ်။​ ဒီနေရာမှာ​ array ထဲက value အရေအတွက်က စုံဂဏန်းမဟုတ်ဘဲ မဂဏန်းဖြစ်နေတာကို သတိထားကြည့်ရပါမယ်။ မဂဏန်းဖြစ်နေတဲ့အတွက် ခွဲလိုက်တဲ့ array ၂ခုမှာ တခုနဲ့ တခု size မတူညီပါဘူး။ တဖက်နဲ့တဖက် ဘယ်ဘက်က ပိုပြီး အရေအတွက် များရမယ်ဆိုတာမျိုး မရှိပါဘူး။ ကျွန်တော်တို့ အဆင်ပြေတဲ့ဘက်မှာ များအောင် သတ်မှတ်လို့ရပါတယ်။

ရလာတဲ့ array တွေကို ကြည့်မယ်ဆို တခုထဲ အဆင့်ကို မရောက်သေးတဲ့အတွက် ထပ်ပြီးတော့ ခွဲတာကို ထပ်လုပ်ပါမယ်။ ဂဏန်းတခုချင်းဆီ ဖြစ်သွားတဲ့အထိ ထပ်ပြီးတော့ ခွဲတာကို လုပ်သွားပါမယ်။

ဒီအဆင့်မှာ ကြည့်မယ်ဆို [6, 12] ဆိုတဲ့ array ကလွဲရင် ကျန်တဲ့ value တွေအကုန် တခုချင်းစီ ခွဲပြီးသွားပြီပဲ ဖြစ်ပါတယ်။ 904 က [6, 12, 904] ကနေ ခွဲလာတာဖြစ်တဲ့အတွက် [6,12] ကို sort လုပ်ပြီးပြီလို့ သတ်မှတ်တော့မှပဲ သူနဲ့ ပြန်ပေါင်းမှာ ဖြစ်ပါတယ်။ ဒီတော့ တခြား value တွေကို sort လုပ်ပြီး ပေါင်းလိုက်ပါမယ်။

အခုအချိန်မှာ 6 နဲ့ 12 ကလဲ တခုချင်းစီ ဖြစ်သွားပြီဖြစ်တဲ့အတွက် သူတို့နှစ်ခုကို sort လုပ်ပြီးပြီလို့ သတ်မှတ်ပြီး ပေါင်းလိုက်ပါမယ်။ ကျန်တဲ့ sort လုပ်ပြီးသားတာတွေထဲမှာ [34,45] နဲ့ [2, 51] ကို နောက်တဆင့်ပေါင်းတာ ဆက်လုပ်ပါမယ်။ [8, 123] ကတော့ သူကိုယ်တိုင် sort လုပ်ပြီးသား ဖြစ်ပေမယ့် တွဲမယ့် 6, 12, 904 sort လုပ်ပြီးပြီလို့ မသတ်မှတ်ရသေးတဲ့အတွက် တချက်စောင့်ပါမယ်။

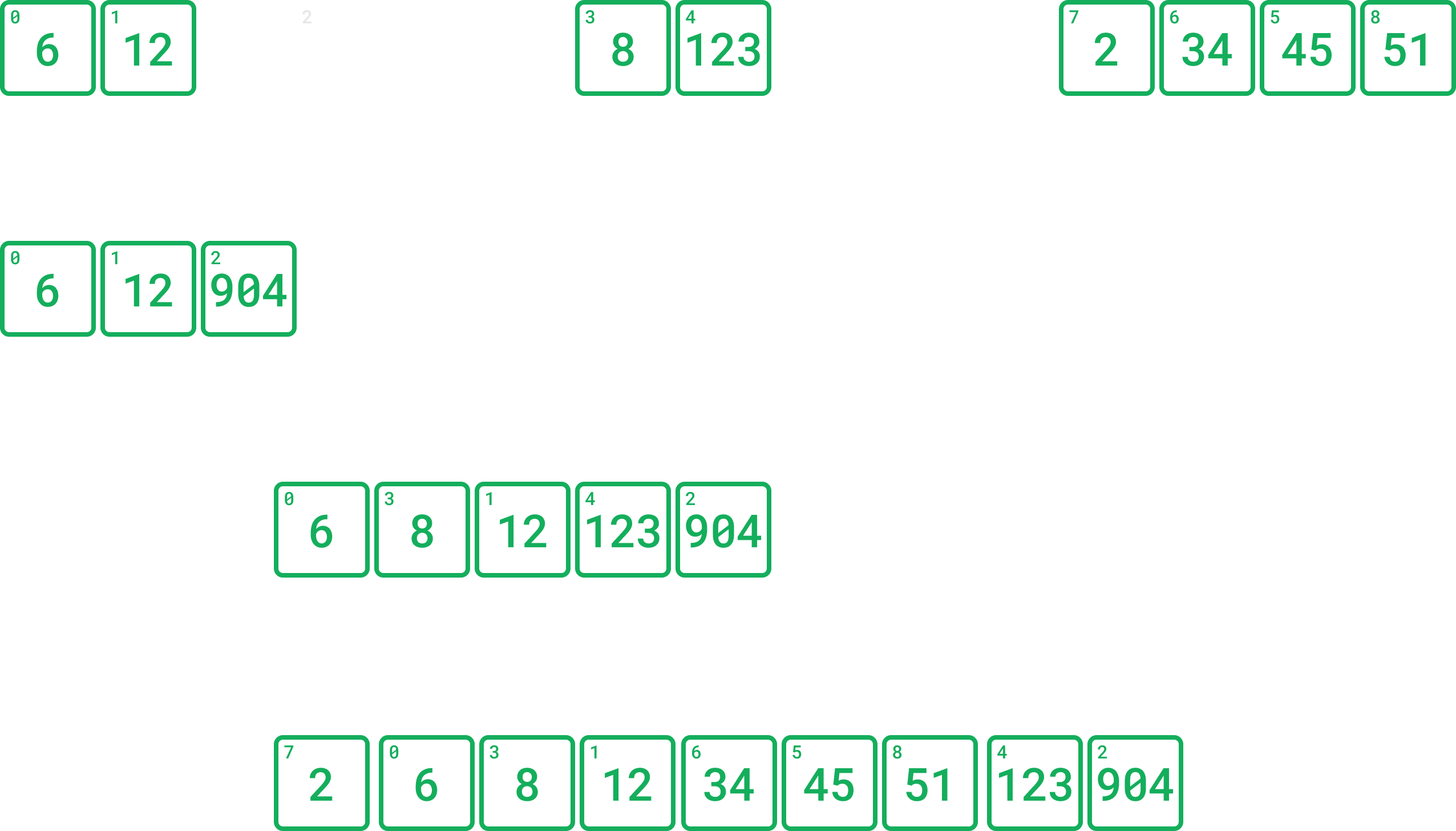
ကျန်တဲ့အဆင့်တွေကတော့ အပေါ်မှာ ပြထားတဲ့အတိုင်းပဲ ဖြစ်ပါတယ်။ [6,12, 904] sort လုပ်ပြီးပြီလို့ သတ်မှတ်ပြီး ပေါင်းလိုက်တဲ့အခါ ကျန်တဲ့ [8,123] နဲ့ ဆက်ပြီး ပေါင်းလိုက်ပါမယ်။ ဒါပြီးရင်တော့ တခြား တစ်ဖက်မှာ ပေါင်းထားပြီးပြီဖြစ်တဲ့ [2,34,45,51] တို့နဲ့ ပေါင်းလိုက်ပါမယ်။

ဒီ merge sort ရဲ့ sort လုပ်ပြီးသား အပိုင်းတွေ ပေါင်းတဲ့အခါ အစီအစဥ်အလိုက် ပေါင်းသွားတာကို သတိပြုမိပါလိမ့်မယ်။ ပေါင်းမယ့် array ၂ခုကို ယှဥ်ပြီးတော့ ငယ်တာကို ဆွဲထုတ်ပြီးတော့ တဆင့်ချင်း ပေါင်းသွားတာမျိုးပဲ ဖြစ်ပါတယ်။

code အနေနဲ့ ဘယ်လို ရေးမလဲကို လေ့လာကြည့်ရအောင်ပါ။

const merge = (array, left, right, mid) => {
  let n1 = left;
  let n2 = mid + 1;
  const temp = [];

  while (n1 <= mid && n2 <= right) {
    if (array[n1] <= array[n2]) {
      temp.push(array[n1]);
      n1++;
    } else {
      temp.push(array[n2]);
      n2++;
    }
  }

  while (n1 <= mid) {
    temp.push(array[n1]);
    n1++;
  }

  while (n2 <= right) {
    temp.push(array[n2]);
    n2++;
  }

  for (let i = left; i <= right; i++) {
    array[i] = temp[i - left];
  }
};

const mergeSort = (array, left, right) => {
  if (left >= right) {
    return;
  }

  const mid = Math.floor((left + right) / 2);
  mergeSort(array, left, mid);
  mergeSort(array, mid + 1, right);
  merge(array, left, right, mid);
};

let items = [6, 12, 904, 8, 123, 45, 34, 2, 51];
console.log(mergeSort(items, 0, items.length - 1));
console.log({ items });

[2,6,8,12,34,45,51,123,904]

Time Complexity

Merge sort ရဲ့ ထူးခြားချက်ကတော့ ဘယ်လို အခြေအနေပဲ ဖြစ်ဖြစ် (worst, best, average cases) တွေမှာ complexity O(n.log n) ကို ရရှိနေမှာပဲ ဖြစ်ပါတယ်။ ဘယ်လို array input ပဲ ဖြစ်ပါစေ ဝင်လာတာနဲ့ တခုချင်းစီ ဖြစ်တဲ့အထိ ခွဲပြီး အစဥ်လိုက် ပြန်စီသွားတာ ဖြစ်တဲ့အတွက် complexities တွေ အတူတူ ရှိနေတာပဲ ဖြစ်ပါတယ်။

Space Complexity

Merge sort ရဲ့ merge လုပ်တဲ့အပိုင်းမှာ temp array ကို create လုပ်ပြီး value တွေကို ထည့်တာကို တွေ့နိုင်ပါတယ်။​ ဒီလို ပေးထားတဲ့ array အပြင် ထပ်ပြီး တည်ဆောက်ရတဲ့အတွက် merge sort ရဲ့ space complexity ကတော့ O(n) ကို ရရှိမှာပဲ ဖြစ်ပါတယ်။