Radix Sort

Radix sort ကတော့ နံပါတ်ကို အခြေခံတဲ့ sort လုပ်နည်း တစ်မျိုးပဲ ဖြစ်ပါတယ်။ နံပါတ်မှာမှ နေရာအလိုက် value တွေကို စီသွားတဲ့ sorting algorithm ပဲ ဖြစ်ပါတယ်။ value တွေကို တခုနဲ့တခု နှိုင်းယှဥ်ပြီး စီတာမျိုး မလုပ်ဘဲ value ရဲ့ နေရာအလိုက် တန်ဖိုးတွေကို bucket တွေထဲ​ထည့်ပြီး စီသွားတာမျိုး လုပ်ပါတယ်။ ဥပမာ 123 က စီရမယ့် ကိန်းဂဏန်းတွေက တခုဖြစ်တယ်ဆို 123 ဆိုပြီး တန်းပြီးတော့ နှိုင်းယှဥ်တာမျိုး မလုပ်ဘဲ ရာဂဏန်း ဖြစ်တဲ့ (၁), ဆယ်ဂဏန်း ဖြစ်တဲ့ (၂), ခုဂဏန်းဖြစ်တဲ့ (၃) ဆိုပြီး ခွဲပြီးတော့ နေရာတခုချင်းစီအတွက် စီတာမျိုး လုပ်သွားမှာ ဖြစ်ပါတယ်။

ဂဏန်းတွေကို နေရာအလိုက် value ပေါ်မူတည်ပြီး bucket တွေထဲ​ ထည့်တာက counting sort ပဲ​ဖြစ်ပါတယ်။​ ဒီတော့ radix sort မှာ counting sort ကိုပါ အသုံးပြုထားတာ ဖြစ်ပါတယ်။ Counting sort ကိုတော့ နံပါတ်ထပ်တာတွေ များများ ပါတဲ့ input array တွေကို စီတဲ့နေရာမှာ သုံးလို့ကောင်းပါတယ်။ counting sort အကြောင်းကို ဒီ article မှာ ဖတ်ကြည့်လို့ရပါတယ်။

Counting Sort

Counting sort ဆိုတာကတော့ နာမည်မှာပါတဲ့အတိုင်းပဲ value တွေကို ရေတွက်တာကို အခြေခံပြီး တည်ဆောက်ထားတဲ့ sorting algorithm တခုပဲ ဖြစ်ပါတယ်။ သူ့ကိုတော့ decimal တွေကို sort တဲ့နေရာတွေ၊ value တူ

Arkar's BlogArkar Min Tun

ကျွန်တော်တို့မှာ စီဖို့အတွက် input array ကို အခုလိုမျိုး ရှိတယ်ဆိုပါစို့။ ဒါကို radix sort သုံးပြီး ဘယ်လို sort လုပ်သွားမလဲ လေ့လာကြည့်ရအောင်ပါ။

မစီခင် input array ထဲမှာ အကြီးဆုံး value က ဘာလဲဆိုတာ တချက်ကြည့်ပါမယ်။ အခု အကြီးဆုံး value က 904 ဖြစ်တဲ့အတွက် သူ့မှာ ဂဏန်းနေရာ ခု, ဆယ်, ရာဆိုပြီး ၃ခုပါဝင်ပါတယ်။ ဒီတော့ input array ကို ၃ကြိမ် loop ပတ်ပြီးတော့ နေရာတခုချင်းစီအတွက် စီသွားပါမယ်။ ဒီထက်ပိုပြီး များတယ်နည်းတယ်ဆိုလဲ သူတို့မှာ ပါဝင်တဲ့ ကိန်းဂဏန်း အရေအတွက်ပေါ်မူတည်ပြီး အတိုးအလျှော့ လုပ်သွားရပါမယ်။

အရင်ဆုံး ခုဂဏန်းနေရာမှာရှိတဲ့ value တွေကို စပြီးတော့ စီပါမယ်။ ခုဂဏန်းမှာ နည်းနေတယ်ဆို value ဘယ်လောက်ပဲ ကြီးနေပါစေ ရှေ့ကိုပို့ထားပြီး များနေတယ်ဆို value ဘယ်လောက် ငယ်နေပါစေ နောက်ကို ပို့ထားပါမယ်။

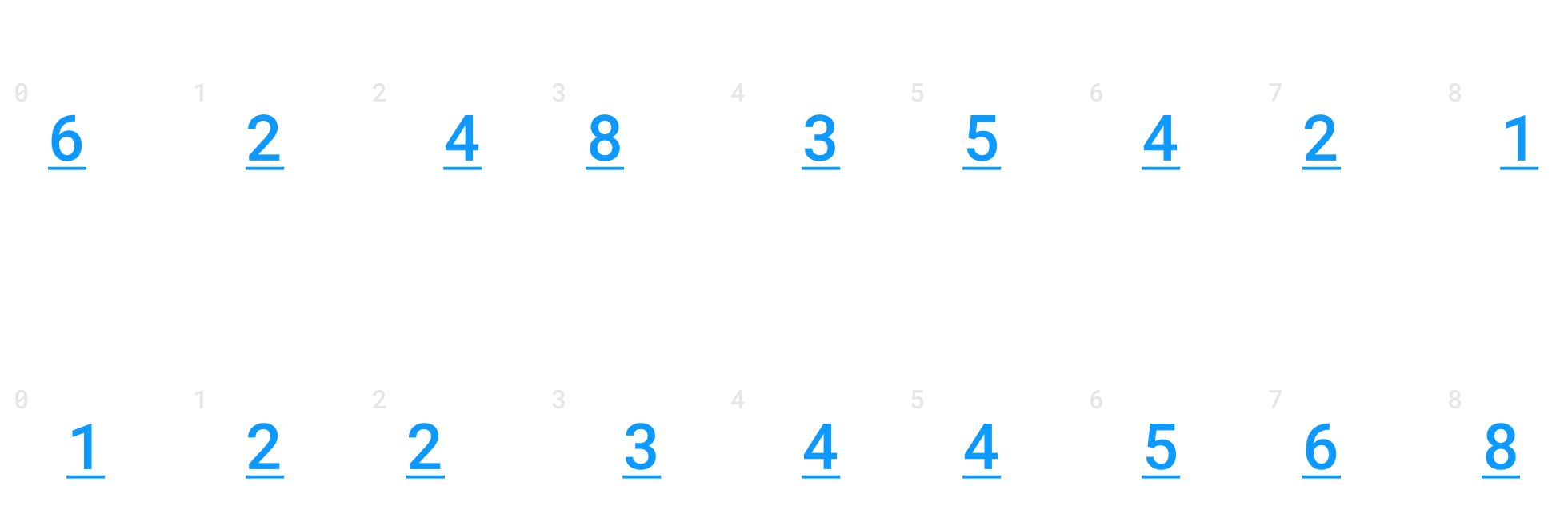
အခုဆိုရင်တော့ ခုဂဏန်းအတွက် စီပြီးသွားပြီပဲ ဖြစ်ပါတယ်။ ဒီတော့ ဆယ်ဂဏန်းအတွက် စီတာကို ဆက်လုပ်ပါမယ်။ တကယ်လို့ အခုစီမယ့်နေရာအတွက် value ရှိမနေဘူးဆိုရင် 0 (zero) အဖြစ်သတ်မှတ်ပြီး ရှေ့ကို ပို့ပါမယ်။

အခု ဆယ်နေရာအတွက်လဲ စီပြီးပြီဆိုတော့ ရာဂဏန်း နေရာကို စီသွားပါမယ်။ အစထဲက input array မှာ ပါတဲ့ အကြီးဆုံး ဂဏန်းကို တွက်ထားပြီးတဲ့အတွက် ၃ခါ စီပြီးသွားရင် sort လုပ်ပြီးတဲ့ array ကို ရရှိရမှာပဲ ဖြစ်ပါတယ်။ အပေါ်အဆင့်ကလိုပဲ ဒီအဆင့်ရဲ့ ရာဂဏန်းနေရာမှာ value မရှိဘူးဆို 0 (zero) အနေနဲ့ သတ်မှတ်ပြီး ရှေ့ကို ပို့သွားမှာပါ။

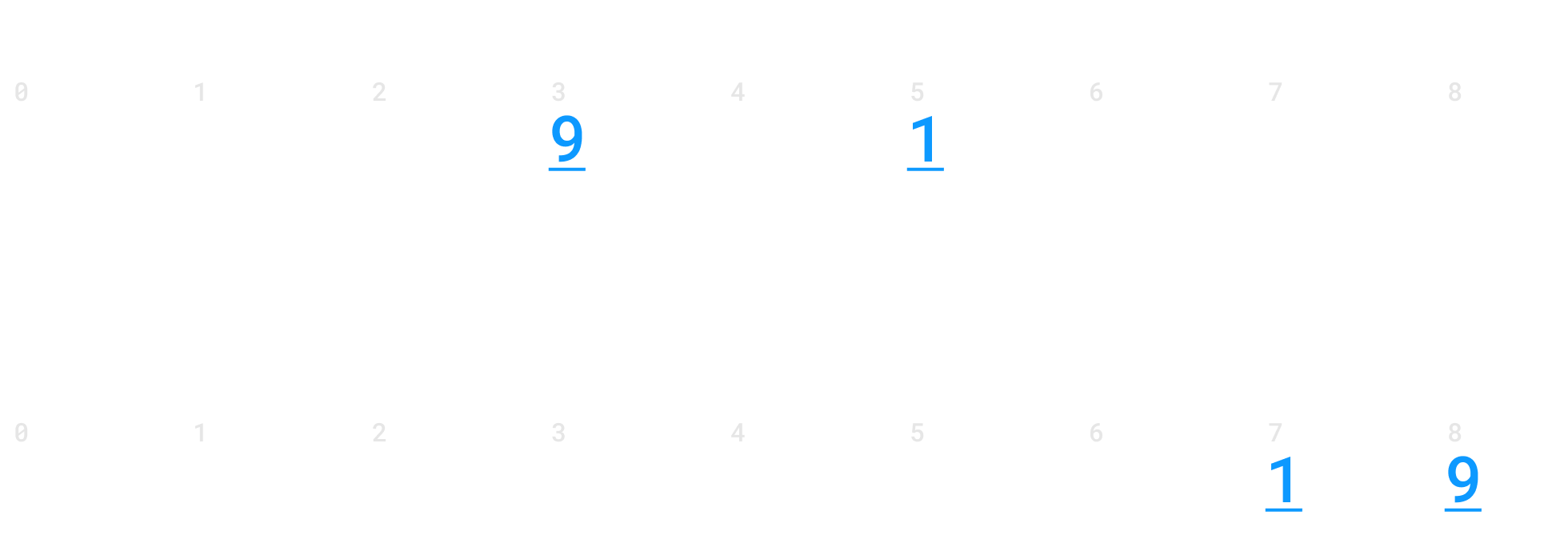
အခုလို အဆင့်ဆင့် ဂဏန်းနေရာအလိုက် စီပြီးသွားရင်တော့ sort လုပ်ထားတဲ့ output array ကို ရရှိပါပြီ။

Code အနေနဲ့ ဘယ်လို ရေးသလဲ​ကြည့်ကြည့်ရအောင်ပါ။

const countingSort = (inputValue, position) => {
  const inputLength = inputValue.length;
  const countArray = new Array(10).fill(0);

  for (let i = 0; i < inputLength; i++) {
    const value = Math.floor(inputValue[i] / position) % 10 ?? 0;
    countArray[value]++;
  }

  for (let i = 1; i < 10; i++) {
    countArray[i] += countArray[i - 1];
  }

  const outputValue = new Array(inputLength);
  for (let i = inputLength - 1; i >= 0; i--) {
    const value = Math.floor(inputValue[i] / position) % 10 ?? 0;
    outputValue[countArray[value] - 1] = inputValue[i];
    countArray[value]--;
  }

  for (let i = 0; i < inputLength; i++) {
    inputValue[i] = outputValue[i];
  }
};

const radixSort = (inputValue) => {
  const max = Math.max(...inputValue);
  for (let position = 1; Math.floor(max / position) > 0; position *= 10) {
    countingSort(inputValue, position);
  }
  return inputValue;
};

let inputValue = [6, 12, 904, 8, 123, 45, 34, 2, 51];
console.log(radixSort(inputValue));

[2, 6, 8, 12, 34, 45, 51, 123, 904]

ဒီမှာကြည့်မယ်ဆို counting sort ကို အဓိကထားပြီး သုံးသွားတာ တွေ့နိုင်ပါတယ်။ တကယ်လဲ​ radix sort ဆိုတာ နေရာအလိုက် counting sort ကို သုံးထားတာ ဖြစ်ပါတယ်။ counting sort အပြင် နားလည်ရမှာက နေရာအလိုက် value တွေ တွက်ထုတ်တာပဲ ဖြစ်ပါတယ်။ အဲ့ဒါဆိုရင်တော့ radix sort ကို ရပါပြီ။

Time Complexity

Radix sort မှာ အဓိကကတော့ value တခုချင်းစီမှာပါတဲ့ ဂဏန်း (digit) အရေအတွက် ဖြစ်ပါတယ်။ ဒီဂဏန်းအရေအတွက်ပေါ်မူတည်ပြီးတော့မှ ကျွန်တော်တို့ ဘယ်နှစ်ခေါက် loop ပတ်မလဲ ဆုံးဖြတ်တာဖြစ်ပါတယ်။ အဲ့ဒါအပြင် value အရေအတွက်နဲ့ counting sort ရဲ့ bucket ထဲထည့်တာတွေကိုလဲ time complexity မှာ ထည့်တွက်ရပါမယ်။​ ဒီတော့ value တခုချင်းစီမှာ ပါတဲ့ ဂဏန်းအရေအတွက်ကို d (number of digit)၊ counting sort ရဲ့ bucket တွေကို b (number of bucket)၊​ input array မှာပါတဲ့ value အရေအတွက်ကို n လို့ သတ်မှတ်မယ်ဆို time complexity O(d(n+b)) ကို ရရှိမှာ ဖြစ်ပါတယ်။

Space Complexity

Radix sort ရဲ့ space complexity ကို ကြည့်မယ်ဆိုရင် loop လုပ်ပြီး counting sort ကို ခေါ်ထားတာ ဖြစ်တဲ့အတွက် counting sort ရဲ့ space complexity ဖြစ်တဲ့ O(n+b) ကို ရရှိမှာပဲ ဖြစ်ပါတယ်။ n ကတော့ input array ထဲမှာ ပါလာတဲ့ value အရေအတွက်ဖြစ်ပြီး b ကတော့ counting sort ထဲမှာ တည်ဆောက်ရမယ့် bucket အရေအတွက်ပဲ ဖြစ်ပါတယ်။